One problem found in the simplest Advection term: Differential Rotation

The last term in the Master Equation,

is the advection term in the toroidal (phi) direction. This term is dealt with the Lax-Wendroff Scheme in the complex (and more accurate) code.

Simple first order accurate Euler scheme goes haywire after a few iterations, and does not conserve the peak of magnetic field (due to numerical diffusion).

But, the Lax-Wendroff scheme, which is second order accurate improves over the Euler Scheme, and preserves the peak of magnetic field, with negligible numerical diffusion.

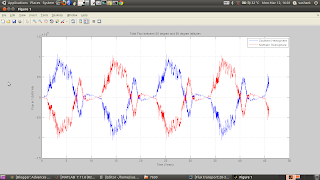
A problem however, generally found with Lax-Wendroff schemes is, that some ripples can be seen behind the travelling wave. The total flux, and the magnetic field are still accurately conserved. But, due to the ripples, the unsigned flux suffers change with time; which is unphysical.

 The simulation of a meridian-like flux tube shows the formation of these ripples.

For a movie of the simulation, play the video named Flux tube1.mp4 after clicking here .

Problem with the Euler Code

While the simulation in last post had sunspots at 22.5 degrees latitude, and their flux was not carried over 80 degrees, the time step of 100 seconds gave us quite accurate flux conservation.

But, for a sunspot placed very near the pole, we need a time step of 0.1 second for a stable numerical evolution. When run with a time step of 0.1 second, the code will approximately run for about 3 years on my laptop to complete the simulation of one solar cycle!

We seriously need to parallelise this code, if it passes all the tests we subject it to.

We also need to verify the solution it gives us, and the timespan, or the simulation time for which the results are reliable and numerically stable.

The Euler Code: Solved Imbalance..but Uncertain Accuracy

The Euler method of solving differential equations is less accurate in predicting the solution than those used in the previous code. This required us to use a smaller time step of 100 seconds for time advancing.

First, I tried only the meridional flow without any diffusion or differential rotation disturbing the magnetic field. And to my surprise, I found, that not only there was no imbalance between the hemispheres, but even the flux within each hemisphere was conserved individually!

It is logically obvious, that for a symmetric initial condition, the flux distribution at any following time should be symmetric across the equator. And so it was!

Then I gave a try to the code with only differential rotation. Still no imbalance, and accurate flux conservation!

The next step was diffusion. The diffusion only code also conserved the flux individually in hemispheres, with almost no imbalance. Sometimes, there would be an imbalance, about 10 million times less than the flux in a sunspot. But then it would become zero again.

And then, I gave a run to the code, with all the 3 effects combined, and following is a screenshot showing:
1st column: Southern Hemisphere Flux
2nd column: Northern Hemisphere Flux
3rd column: Imbalance.

I also took the liberty of making a movie of the simulation, to see the flux reach the poles in 3D! The 3D plotting was one of the best things I did while in Montana.. :)

This movie was made from a simulation that runs for about 2 years in the code, and ran for about 24 hours on my laptop!

 

The video quality degraded while uploading it here. For 1080p Full HD version of the video, click here .

The Imbalance Problem

Finally, some results are here, after my workstation laptop suffered 3 reinstallations of all operating systems in 3 days!

Its good to be back after an awesome summer in Montana.

A lot of new things were tried after the last post. The major concern, however was "THE IMBALANCE" of flux which we observed.

We observed that the flux in a sunspot increases/decreases rapidly as it moves around and diffuses. The problem still hasn't been completely resolved yet.

But, to see what is wrong with the code, I tried writing a simpler version of the code following the simple Euler method of solving differential equations and simple finite difference scheme.

It was thought, that this code will be quite accurate atleast for the first few iterations, and can be used to calliberate and validate the results from the full fledged code with various numerical schemes. For simplicity, I will call the simpler code (new) the 'Euler Code' and the previous code the 'Complex Code'.

Here is an example of the problem of Imbalance:
With one sunspot each in both the hemispheres, the following screenshot shows the flux values evolving over time.
1st column: Southern Hemishpere Flux
2nd column: Northern Hemisphere Flux
3rd column: Flux imbalance between the 2 hemispheres.

Calculating the Flux Transported in different regions on the surface

Posting some results on my Birthday!

A simulation was run yesterday, with a modified profile of no. of BMRs (Unsigned Flux=2X10^21 Mx) errupting V/s time as below:

Total BMRs per cycle: 7630

The total flux between 2 latitudes was calculated by integrating the product of longitudinally averaged magnetic field and the area of a grid element at that latitude.

                              Flux=Sum[Bavg(lat)*area(lat)]

Flux between any 2 latitudes was thus calculated at regular intervals, and the difference between flux at 2 different times would give us the change in flux, meaning the flux transported. This difference can be interpreted as flux flowing in the concerned region. It can be both positive and negative.

                                                     BUTTERFLY DIAGRAM

                                                     Peak Polar Field: +/- 11 Gauss

The initial polar field in the northern hemisphere was negative, and that in the southern hemisphere was positive.

1. 0-5 :

So, the flux transported to the equator from above 5 degrees latitude would be negative in the northern hemisphere, and positive in the southern. This flux gets cancelled across the equator.

Remember that the calculation of flux transport here, shows the net flux flowing into the concerned region. So, this plot suggests that there is a flow of negative flux(leading polarity) into the northern region, and flow of positive flux(leading polarity) into the southern region. Both flow towards the equator, where these fluxes cancel each other.

The net flux in the region of 5 degrees from the equator can reach the order of 1-2 sunspots.

2. 10-20 :

The flux transport from 10-20 degree latitudes is negative in the northern hemisphere initially, and then becomes positive after half cycle. This is because the BMRs errupt at higher latitudes initially, hence the leading polarity crosses this region on its way to the equator. But, later on, BMRs start appearing at lower latitudes, which results in a net transfer of trailing polarity flux to the poles.

The net flux in this region can reach the order of  1.5X10^22 Mx.

3. 20-30 :

The trailing polarity flux from lower latitudes enters this region, signified by positive peaks in the northern hemisphere (1st cycle) and negative peaks in the southern hemisphere. 

 

The net flux in this region can reach the order of  4X10^21 Mx.

4. 30-40 :

In this region, there is just about no erruption of BMRs. So, this is like a come and go region for flux. The plot here is plotted with the unsigned difference in net flux for simplicity. Positive peaks indicate the trailing polarity flux entering the region, and negative peaks indicate, that a net flux from leading polarities has entered the region. Overall, there is a negligible storage of trailing polarity flux in this region. 

The net flux in this region can reach the order of 6X10^21 Mx. 

5. 40-50 :

There is a lot of addition and subtraction of flux in this region during a solar cycle. A positive peak in the flux transport (1st cycle) indicates the trailing polarity reaching the region, and negative peak indicates that the leading polarity flux has entered the region. Overall, there is a small net accumulation of flux from the trailing polarity in this region. 

The net flux in this region can reach the order of  8X10^21 Mx.

6. 50-60 :

This region comprises partly of the polar field. The plot shows, that there is always a positive net flux reaching this region in the first cycle, which cancels the previous field, and builds up a new one. Then, for the next cycle, there a negative flux reaching this region at all times. So, the net flux in this region does not show more than one peak. If it is increasing, it will increase till the highest value, and if it is decreasing, it will decrease till the lowest value. 

The net flux in this region can reach the order of  2.5X10^22 Mx.

2 Different Butterfly Diagrams

All the Butterfly diagrams till now were plotted with latitude on the y axis, and time on the x axis. But normally data analysts plot the butterfly diagrams with sine of the latitude on the y axis.

This post is to show what difference is created by changing the axis.

                                                           Latitude V/s time butterfly plot

                                                        Sin(Latitude) V/s time butterfly plot

We can see that in the latter plot, the area from 0 to 60 degree latitude has been magnified, and the area from 60 to 90 degrees latitudes has been compressed near the poles.

Summary of the effect of variation of sunspot paramters

The difference in the peak polar field in consecutive solar cycles varies with different parameters of BMRs as:

1. TILT ANGLE:

Standard tilt angle: 19 degrees (van Ballegooijen et al.)

2. SEPARATION:

Standard separation: Unknown

3. NO. OF SUNSPOTS PER CYLCLE:

Standard no. of sunspots per cycle: Unknown

Observations show the difference in the peak polar field to be around 20 Gauss. Now, several combinations of variations in these parameters can lead us to that difference.

Effect of varying separation in BMRs on the strength of Solar Cycle

The separation between the spots in a BMR has a significant effect on the strength of the Solar cycle.
R is the radius of individual sunspots, and 2 sunspots in a BMR are identical, except that they have magnetic field of opposite polarity. All the distances are between centers of sunspots.
1 unit distance=1000km
snomax=200
tilt=lat/2 with sd=19 degrees
Bmax as per Jiang et al.
Initial polar field= 3.5G, since this value gives stable(equal) oscillations for no change in parameters.

1. Separation= 2R-10

The magnetic field oscillates between +0.84 G and -2.55 G.
Difference= 3.39 G


2. Separation= 2R-5

The magnetic field oscillates between +1.6 G and -2.54 G.
Difference= 4.14 G

3. Separation=2R

The magnetic field oscillates between +2.65 G and -2.55 G.
Difference= 5.20 G

4. Separation= 2R+10

The magnetic field oscillates between +4.011 G and -2.50 G.
Difference= 6.51 G

5. Separation= 2R+20

The magnetic field oscillates between +5.56 G and -2.47 G.
Difference= 8.03 G

6. Separation= 2R+30

The magnetic field oscillates between +6.85 G and -2.45 G.
Difference= 9.30 G


Internal flux cancellation depends on the separation between the 2 spots in a BMR. The greater the separation, less is the cancellation, and more flux is transported towards the poles. Clearly affecting the strength of the cycle.

For every value of separation, there will be a different value of initial polar field, for which we will obtain an oscillation with same magnitude on either side of zero. But the difference between the peaks will stay the same, as previous simulations suggest.

Modified Separation

All the previous simulations were for  a larger separation between 2 sunspots in a BMR, so that maximum flux is differentially transported.

But now, to study the effect of varying the no. of sunspots per cycle, we need to fix the separation at some value.

For the next post, that will cover the variation of peak magnetic field with respect to variation in no. of errupting BMRs in a cycle, the separation will be fixed such that, the 2 sunspots in a BMR grace each other's boundaries. i.e. separation between their centres is twice their radius. For such a separation, stabilised oscillation is obtained for:

Initial field=3G
The field oscillates between +2.20 and -2.21G
Difference=4.41G

Note: This post should have been before the one below.
The post showing the effect of varying sunspot nos. is below.

Running the code with different number of BMRs per cycle

The code was run with different values of input BMRs per cycle, and the initial field was varied for each run to get a stable oscillation. The results are:

1. No. of BMRs per cycle = 7028,  with a peak of 200 BMRs@5.5 yrs.

Initial field = 3.5G
The field oscillates between +2.65G and -2.55G
Difference=5.20G

2. No. of BMRs per cycle = 10722, with a peak of 300 BMRs@5.5 yrs.

Initial field = 5G
The field oscillates between +3.81G and -3.64G
Difference=7.45G

3. No. of BMRs per cycle = 14412, with a peak of 400 BMRs@5.5 yrs.

Initial field = 7G
The field oscillates between +5.31 and -5.10
Difference= 10.41G

4. No. of BMRs per cycle = 18082, with a peak of 500 BMRs@5.5 yrs.

Initial field = 10G
The field oscillates between +6.58 and -7.25
Difference=15.85G

5. No. of BMRs per cycle = 21768, with a peak of 600 BMRs@5.5yrs.

Initial field = 12G
The field oscillates between +8.66 and -8.66G
Difference=17.32G


6. No. of BMRs per cycle = 25442, with a peak of 700 BMRs@5.5yrs.

Initial field = 13.5G
The field oscillates between +10.14 and -9.75G
Difference=19.89G


Ideally, the Sun's peak magnetic field near the poles has a magnitude of about 10G. So, keeping the separation between 2 spots in a BMR to be minimum, so that they just grace each other, we obtain a field of about 10 G in the last case.